Usaremos los datos contenidos en CPS1985 tomados de Berndt (1991). Después de tener disponibles los datos vía data(), podremos tener alguna información a través de la función str(). Todo este análisis fue tomado de Kleiber y Zeileis (2008). Descarga los códigos usados en este post aquí
> str(CPS1985)
'data.frame': 533 obs. of 11 variables:
$ wage : num 4.95 6.67 4 7.5 13.07 ...
$ education : int 9 12 12 12 13 10 12 16 12 12 ...
$ experience: int 42 1 4 17 9 27 9 11 9 17 ...
$ age : int 57 19 22 35 28 43 27 33 27 35 ...
$ ethnicity : Factor w/ 3 levels "cauc","hispanic",..: 1 1 1 1 1 1 1 1 1 1 ...
$ region : Factor w/ 2 levels "south","other": 2 2 2 2 2 1 2 2 2 2 ...
$ gender : Factor w/ 2 levels "male","female": 2 1 1 1 1 1 1 1 1 1 ...
$ occupation: Factor w/ 6 levels "worker","technical",..: 1 1 1 1 1 1 1 1 1 1 ...
$ sector : Factor w/ 3 levels "manufacturing",..: 1 1 3 3 3 3 3 1 3 3 ...
$ union : Factor w/ 2 levels "no","yes": 1 1 1 1 2 1 1 1 1 2 ...
$ married : Factor w/ 2 levels "no","yes": 2 1 1 2 1 1 1 2 1 2 ...
>
Esta salida revela que CPS1985 es un “data.frame” compuesto por 533 observaciones y 11 variables, incluyendo la variable numérica (continua) wage, las variables numéricas (enteras) education, experience, and age y siete “factores” (variables categóricas, llamadas Factor en R) cada una con 6 categorías (las categorías son llamas niveles (levels) en R).
En vez de utilizar la vista tipo lista que nos proporciona la función str(), es más usual inspeccionar el inicio y el final de la base de datos (data.frame) en su forma natural, es decir, como un arreglo rectangular de valores. Para este objetivo existen funciones apropiadas tales como head() y tail() que nos proporcionan (por defecto) las primeras 6 observaciones y las últimas 6 observaciones de cada variable, respectivamente. Así por ejemplo,
head(CPS1985) wage education experience age ethnicity region gender occupation
1 4.95 9 42 57 cauc other female worker
2 6.67 12 1 19 cauc other male worker
3 4.00 12 4 22 cauc other male worker
4 7.50 12 17 35 cauc other male worker
5 13.07 13 9 28 cauc other male worker
6 4.45 10 27 43 cauc south male worker
sector union married
1 manufacturing no yes
2 manufacturing no no
3 other no no
4 other no yes
5 other yes no
6 other no no
>
Por razones de espacio no se presenta el resultado de aplicar tail(CPS1985), pero el lector lo puede ejecutar y verá que la información que proporciona es muy semejante a head(CPS1985), la diferencia es que tail() da las últimas 6 filas como se ha señalado antes.
Otra manera apropiada y rápida de obtener un resumen de la información contenida en la base de datos es a través de la función summary() la cual proporciona un resumen por cada una de las variables.
> summary(CPS1985) wage education experience age
Min. : 1.000 Min. : 2.00 Min. : 0.00 Min. :18.00
1st Qu.: 5.250 1st Qu.:12.00 1st Qu.: 8.00 1st Qu.:28.00
Median : 7.780 Median :12.00 Median :15.00 Median :35.00
Mean : 9.031 Mean :13.03 Mean :17.82 Mean :36.84
3rd Qu.:11.250 3rd Qu.:15.00 3rd Qu.:26.00 3rd Qu.:44.00
Max. :44.500 Max. :18.00 Max. :55.00 Max. :64.00
ethnicity region gender occupation sector
cauc :440 south:156 male :289 worker :155 manufacturing: 98
hispanic: 26 other:377 female:244 technical :105 construction : 24
other : 67 services : 83 other :411
office : 97
sales : 38
management: 55
union married
no :437 no :184
yes: 96 yes:349
Dado que en lo sucesivo de esto post se utilizará repetidamente la base CSP1985, trataremos de evitar usar comandos muy extensos como CSP1985$education para ello separaremos cada variable de la base de datos y así podremos acceder a ella directamente por su nombre sin necesidad de anteponer el nombre de la base donde están contenidas, para lograr eso haremos uso de la función attach(). Además para evitar escribir muchas letras, renombraremos y abreviaremos los nombres de dos niveles (categorías) de la variable occupation, cambiaremos “techcnical” por “techn” y “management” por “mgmt”.
> levels(CPS1985$occupation)[c(2,6)]<-c("techn", "mgmt") > attach(CPS1985)
Ahora las variables son accesibles por sus nombres.
Es hora del análisis, procederemos con él ilustrando cómo se hace una análisis exploratorio considerando una sola variable, luego pares de variables, haciendo la distinción entre variables numéricas, factores (categóricas) y combinaciones de ambas. Empezamos con el caso más simple, considerando una única variable.
Sólo una variable numérica
Empezaremos dando una mirada a la distribución de los salarios de la muestra, esto es la variable wage> summary(wage)
Min. 1st Qu. Median Mean 3rd Qu. Max.
1.000 5.250 7.780 9.031 11.250 44.500
La función summary() proporciona un resumen de seis números: el valor mínimo, el primer cuartil, el segundo cuartil (=mediana), el tercer cuartil, el valor máximo y el valor medio de la distribución. La media y la mediana también se pudieron haber obtenido de la siguiente manera
> mean(wage)
[1] 9.031426
> median(wage)
[1] 7.78
y la función fivenum() calcula un resumen de las cinco medidas de posición no central listados anteriormente. En tanto que, min() y max() habrían proporcionado el mínimo y el máximo valor de la distribución. Los cuartiles se podrían haber obtenido usando quantile().
Para las medidas de dispersión, existen las funciones
> var(wage) [1] 26.43096
> sd(wage)
[1] 5.141105
que nos devuelven el valor de la varianza y el de la desviación típica (desviación estándar según guste llamarla).
Los resúmenes gráficos también son muy útiles. Para variables numéricas como el caso de wage, las visualizaciones de densidad (vía histogramas o “kernel smoothing”) y los diagramas de caja son adecuados. Los diagramas de caja se considerarán cuando se nos refiramos a análisis de dos variables. La Figura 1, obtenida vía
par(mfcol=c(1,2))

hist(wage, freq=F)
hist(log(wage), freq=F)
lines(density(log(wage)), col=4)
muestra las densidades de wage y su logaritmo (esto es, el área bajo la curva es igual a 1, resultando del hecho de freq=FALSE; de otra manera las frecuencias absolutas habrían sido dibujadas). En el panel derecho de la Figura 1 se ha añadido al histograma la densidad kernel estimada a partir de la función density(). Claramente, la distribución de los logaritmos es menos sesgada que la de los datos originales (datos brutos). Note que density() sólo calcula las coordenadas de la densidad pero no la grafica, por eso esta estimación es agregada usando la función lines().
Figura 1. Histogramas de wages (izq.) y de su logaritmocon densidad superpuesta (derecha)
Sólo una variable categórica
Para datos categóricos, no tiene mucho sentido calcular la media ni la varianza; en su lugar, lo que necesitamos es una tabla que nos indique las frecuencias con las cuales las categorías ocurren. Si a R se le dice que cierta variable es categórica (haciéndola un “factor”), él automáticamente escogerá el resumen adecuado:
> summary(occupation) worker techn services office sales mgmt
155 105 83 97 38 55
Esto también pudo haber sido calculado a través de table(occupation). Si en lugar de las frecuencias absolutas, lo que se desea son las frecuencias relativas, entonces existe la función prop.table() que lo hace.
> prop.table(tab)
occupation
worker techn services office sales mgmt
0.29080675 0.19699812 0.15572233 0.18198874 0.07129456 0.10318949
Las variables categóricas con comúnmente visualizadas mediante diagramas de barras, los gráficos de pastel también son útiles. Ejemplo,
> barplot(tab)
> pie(tab)
Figura 2. Diagrama de barras y de pastel de occupation
Note cómo ambas funciones utilizan las frecuencias como input. Utilizando la función plot(occupation) se logra lo mismo que se logró con barplot(table(occupation)), estos procedimientos son equivalentes, pero usando plot() se va directamente al gráfico no hay cálculos intermedios como los hay si se utiliza barplot() en la que primero se debe calcular la tabla de frecuencias.
Dos variables categóricas
La relación entre dos variables categóricas es frecuentemente resumida en una tabla de contingencia. Estas tablas pueden ser creadas ya sea con xtabs() una función que requiere de una fórmula de interface o con table(), que es una función que toma arbitrariamente un número de variables para la tabulación cruzada . Consideremos los factores (variables categóricas) occupation y gender para ilustrar: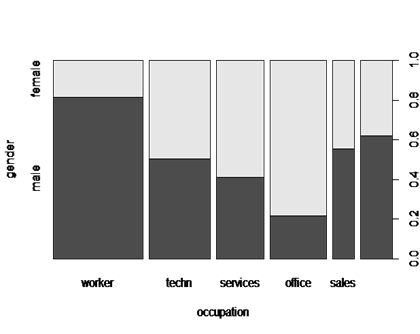
> xtabs(~ gender + occupation, data=CPS1985) 
occupation
gender worker techn services office sales mgmt
male 126 53 34 21 21 34
female 29 52 49 76 17 21
Lo cual pudo haber sido creado de forma equivalente con table(gender, occupation). Una simple visualización de esto es a través de un “mosaic plot” (Hartigan y Kleiner 1981; Friendly 1994), el cual es visto como una generalización de los gráficos de columnas apiladas. El gráfico dado en la Figura 3 (también conocido como “spine plot”, que es una variante de la presentación estándar de la forma estilo mosaico), se obtuvo vía
Figura 3. Mosaic plot (spine plot) de gender vs occupation
> plot(gender~occupation, data=CPS1985)
La Figura 3 muestra que la proporción de hombres y mujeres cambia considerablemente entre las categorías de ocupación (niveles de occupation). Además de las partes sombreadas que nos muestran la distribución condicional del género (gender) dada la ocupación (occupation), la anchura de las barras ofrecen la distribución marginal de la ocupación, indicando que hay comparativamente muchas personas en la categoría “workers” y menos en “sales”, es decir más obreros que vendedores.
Dos variables numéricas
Ejemplificaremos el análisis exploratorio de la relación entre dos variables numéricas utilizando las variables wage y education.
Una medida de relación entre dos variables numéricas es el coeficiente de correlación implementado en la función cor(). Sin embargo, el coeficiente de correlación estándar de Pearson no es muy significativo cuando estamos ante variables con un pronunciado sesgo positivo como es el caso de wage, de manera que calcularemos una versión no paramétrica del coeficiente de correlación, usaremos la correlación de Spearman, la cual está disponible en la función cor() como una opción.
> cor(log(wage), education) [1] 0.3790093
> cor(log(wage), education, method="spearman")
[1] 0.3797895
Figura 4. Diagrama de dispersión de wage (en logs) vs education
Ambas medidas son virtualmente idénticas e indican sólo una modesta correlación entre las variables, veamos el correspondiente diagrama de dispersión en la Figura 4.
> plot(log(wage)~ education)
Una variable numérica y una variable categórica
Es común tener tanto variables numéricas como categóricas en un data frame. Por ejemplo, en nuestro caso tenemos wage y gender y podría haber algún interés en saber la distribución del salario dado el género. Una función adecuada para resumir este tipo de datos combinados es tapply(). Esta función aplica a la variable numérica que es su primer argumento una clasificación según la variable categórica que es su segundo argumento y a la vez aplica la respectiva función que hayamos establecido, esto es el tercer argumento de la función tapply(). Así por ejemplo, es posible obtener la media de los salarios condicionado al género de la siguiente manera
> tapply(log(wage), gender, mean) male female
2.165286 1.935287
Usando comandos similares pueden obtenerse más estadísticos descriptivos o incluso se puede obtener un resumen completo, basta con sustituir summary en el lugar de mean y se obtendrá
> tapply(log(wage), gender, summary)
$male
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.000 1.792 2.189 2.165 2.565 3.269
$female
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.5596 1.5510 1.9230 1.9350 2.3030 3.7950
Adecuadas salidas gráficas para estos datos tales como diagramas de cajas y diagrama cuartil-cuartil (quantile-quantile plot, qq-plot) se presentan en la Figura 5.

Figura 5. Diagrama de Cajas y QQ plot de wage estratificado por gender
Los comandos plot(y~x) y boxplot(y~x) proporcionan el mismo resultado si x es un factor (variable categórica), así pues
plot(log(wage)~gender)
proporcionará la parte izquierda de la Figura 5. Este muestra que las distribuciones son bastante similares en su forma pero con la salvedad que los hombres disfrutan de una ventaja substancial, especialmente los del rango medio. Este último aspecto es corroborado por el QQ-plot que está a la derecha de la Figura 5 el cual resulta de ejecutar la siguiente secuencia de comandos
mwage <- subset(CPS1985, gender=="male")$wage fwage <- subset(CPS1985, gender=="female")$wage
qqplot(mwage, fwage, xlim=range(wage), ylim=range(wage),
xaxs="i", yaxs="i", xlab="male", ylab="female")
abline(0,1)
donde la mayoría de puntos están debajo de la línea diagonal (la cual corresponde a una idéntica distribución en ambas muestras). Este gráfico nos dice que para la mayoría de cuantiles, el salario de los hombres es mayor que el de las mujeres.
Acabamos este post volviendo a unir todas las variables en una sola base de datos con
detach(CPS1985)
Referencias
Dalgaard P (2002). Introductory Statistics with R. Springer-Verlang, New York.Friendly M (1994). Mosaic Displays for Multi-Way Contingency Tables. Journal of the American Statistical Association, 89, 190-200.
Hartigan J A, Kleiner B (1981). Mosaics for Contingency Tables. In W" Eddy (ed.), “Computer Science and Statistics: Proceedings of the 13th Symposium on the Interface”, pp. 268-273. Springer-Verlang, New York.
Kleiber y Zeileis (2008). Applied Econometrics with R. Springer. New York.
Jilber Urbina.

No hay comentarios:
Publicar un comentario